确定信度可以接受的水平(记数据),一般原则是:当rxx <0.70时,测验不能用;当 0.70 ≤ rxx <0.85时,可用于团体比较;当rxx ≥0.85时,才能用来鉴别或预测个人成绩或作为。

　　2.解释个人分数的意义:从信度可以解释个人分数的意义,这就是测量标准误的应用。它有两个作用:

　　⑴估计真实分数的范围：

　　⑵了解实得分数再测时可能的变化情形：

　　例：假设在一个智力测验中，某个被试的IQ为100，这是否反映的他的真实水平?如果再测一次，他的分数将改变多少?已知该智力测验的标准差为15，信度系数为0.84，则其IQ的测量标准误码和可能范围分别为：

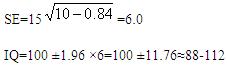
　　我们可以说这个被试的真实IQ有95%的可能性落在88-112之间。即若再测一次，他的智商低于88、高于112的可能性不超过5%。

　　3.比较不同测验分数的差异：差异分数的标准误问题，其公式为：

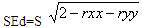
　　例：某被试在韦氏成人智力测验中言语智商为102，操作智商为110.已知两个分数都是以100为平均数，15为标准差的标准分数。假设言语测验和操作测验的分半信度分别为0.87和0.88.问：其操作智商是否显著高于言语智商呢?

　　首先计算出差异分数的标准误：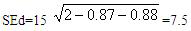

　　在统计上，经常要求两个分数的差异程度达到0.05即5%的显著水平，才能承认不是误差的影响。因此，将差异标准误(7.5)乘以1.96，结果为14.7，这表明个体在韦氏测验两半得分的差异高于大约15分，才能达到0.05的显著水平。上述被试的差异分类为110-102=8是不显著的。

　　洛德提出在学绩测验中，为了保持其可靠性，各类选择题的理想平均难度为：五择一，0.70;四择一，0.74;三择一，0.77;是非题，0.85.